Nowe auto

Ach, ile bym dał to,
By mieć nowe auto.
Jak wiele bym zniósł,
By mieć nowy wóz.

Dałbym złota górę,
By mieć nową furę.
Całą swą krwawicę
Poświęciłbym bryce.

Byłoby wspaniale !
Tak, to prawda, ale
Mam za mały dochód,
By kupić samochód.

Przekręcanie słów

Człowiek jest w stanie bez trudu odczytać tekst, w którym wprowadzone zostały błędy - język ludzki jest nadmiarowy. Poniżej znajduje się przycisk, który miesza tekst widoczny na ekranie w sposób, który pozwala jednak go odczytać.

Sztuczka polega na tym, żeby za bardzo tego tekstu nie pomieszać. Dozwolona jest zamiana blisko położonych liter, przy czym pierwsza i ostatnia litera wyrazu powinny pozostać na swoich miejscach. Tak zakłócony kod mózg ludzki jest w stanie odszyfrować. Zobacz, co stanie się, jeśli dopuscimy większy stopień pomieszania liter.

Wiedza w bazie danych

Czy może istnieć baza danych, zawierająca całą ludzką wiedzę, którą można przeszukiwać za pomocą języka zapytań podobnego do SQL ?

Coś takiego jest celem badaczy sztucznej inteligencji. Taką bazę danych nazywa się ontologią - i trzeba przyznać, że chociaż nie posiadamy jeszcze efektu końcowego - superinteligentnego robota, który odpowiada na wszystkie pytania, to jednak dotychczasowe wyniki badań są imponujące.

Przyjrzałem się ostatnio YAGO (Yet Another Great Ontology), jest to projekt nadający się do tego, by się z nim zapoznać, nawet, jeśli jest się amatorem w tych dziedzinach - posiada interfejs online-owy i względnie przystępny opis.

Sztuczna inteligencja z jednej strony powinna umieć porozumiewać się w języku naturalnym (to też ciekawa i dość już nawet zaawansowana dizedzina) ale przede wszystkim musi być wyposażona w wiedzę, którą określamy jako "common sense", czy "zdrowy rozsądek". Pewne podstawowe informacje są dla nas oczywiste, ale dla komputera nigdy - nawet najprostsze pojęcia i kategorie, którymi się posługujemy muszą być jakoś zaprogramowane.

Mamy Wikipedię - zawiera ona olbrzymie ilości danych, ale nie są ściśle skategoryzowane ani sparametryzowane. Zawiera jednak jakieś
kategorie (choć autorzy YAGO podają przykłady trudności: Elvis należy
do kategorii "Grammy Awards", choć nie jest NAGRODĄ a jej laureatem ...)
oraz INFOBOKSY - które są krokiem w kierunku uściślenia struktury danych.

Autorzy YAGO skorzystali z tych danych i z sieci semantycznej zawartej w WordNet (słownik języka angielskiego wyposażony w hierarchię powiązań semantycznych). Z połączenia tego powstała ontologia YAGO - można ją zapytać np. o polityków będących naukowcami, urodzonych w Hamburgu po roku 1900, albo o firmy założone w Berlinie przed 1970.

Nie jest to, jak się okazuje, jedyny tego typu projekt, jest ich już sporo, istnieje także bogata literatura na temat ontologii specjalistycznych.

YAGO i WordNet są dobrymi miejscami, gdzie można zajrzeć, nawet jeśli się nie zajmuje sztuczną inteligencją na co dzień, ale chce się
zapoznać z tym tematem, choćby pobieżnie.

Rodzaje organizmów

W dzieciństwie dowiadujemy się, że żywe organizmy dzielą się na rośliny i zwierzęta i z niejakim zdziwieniem, ale też z radością przyjmujemy do wiadomości, że my (ludzie) też należymy do zwierząt.

Potem dowiadujemy się o bakteriach - dawniej uczono, że są one roślinami, ale dziś już wiemy, że nie. Nie są też jednak zwierzętami - cała sprawa jest skomplikowana, bo chcąc odpowiedzieć na pytanie, czy bakteria jest zwierzęciem, musimy sami zdefiniować, co rozumiemy, co chcemy rozumieć przez zwierzę.

A są jeszcze wirusy - coś, co nawet nie wiadomo, czy jest żywe, ale składa się z białek i kwasów nukleinowych i jakoś tam prawie żyje. O wirusach dowiadujemy się też dość wcześnie.

Stan obecnej wiedzy na temat klasyfikacji żywych organizmów jest mniej więcej następujący:

Wszystkie organizmy żywe na naszej planecie (a wielu naukowców sądzi, że na innych również) składają się z podstawowych elementów - komórek - które mają wiele cech wspólnych, ale są też bardzo zróżnicowane. Zbudowane są z białek, tłuszczy i czegoś tam jeszcze i potrafią się powielać (rozmnażać, kopiować) dzięki skomplikowanym reakcjom chamicznym z udziałem kwasów nukleinowych RNA i DNA.

Niektóre z tych organizmów składają się z jednej komórki, (jednokomórkowce) a niektóre z wielu (wielokomórkowce). Komórki te (w zależności od gatunku organizmu) mogą być proste, lub bardziej skomplikowane, mogą zawierać pewne podstruktury, będące same jakby mini-komórkami.

Istnieje wielka grupa organizmów (należą do niej rośliny, zwierzęta i my), których komórki zawierają jądro - dużą wydzieloną strukturę, w której zachodzą ważne reakcje i która steruje komórką. Są to eukarionty. Nie-eukarionty to prokarionty - są prostsze i o ile wiem, zawsze jednokomórkowe. To właśnie do nich należą bakterie.

Eukarionty podzielono początkowo na protisty, grzyby, rośliny i zwierzęta. Grzyby na poziomie komórkowym bardziej przypominają zwierzęta niż rośliny. Protisty to szeroka kategoria pierwotniaków, do której zaliczono wszystko, co nie jest grzybem, rośliną lub zwierzęciem. Podział ten był długo uznawany i dlatego jest popularny - dzisiaj oceniany jest raczej jako sztuczny.

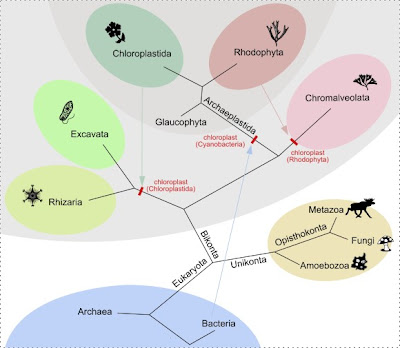
Obowiązująca obecnie klasyfikacja eukariontów bazuje na dokładniejszej wiedzy o budowie ich komórek i opiera się na sześciu "supergrupach" (Opisthokonta, Amoebozoa, Excavata, Rhizaria, rośliny i Chromalveolata). Zwierzęta i grzyby (razem z paroma jeszcze innymi kladami przynależą do supergrupy Opisthokonta.

Oto (pochodzący z zasobów Wikimedia Commons) schemat podziału eukariontów:

rys: Agnieszka Kwiecień, licencja: CC-BY 3.0

Cegła i piórko, czyli co to jest równanie

Jesteś wykształcony ? A czy wiesz, co to są równania - i po co są równania, do czego służą ?

Chociaż każdy z grubsza wie, co to jest równanie, sporo ludzi nie ma wyrobionej intuicji dotyczącej ich użycia - układania i rozwiązywania.

Tymczasem pewne proste reguły matematyki może pojąć kaźdy, skoro uczy się ich dzieci w szkole ...

Równanie to sposób zapisu związku między wielkościami, o których mówimy - tak, by łatwo było nam o nich wnioskować. W życiu spotykamy się z licznymi problemami, które upraszczają się znacznie, jeśli zastosujemy równanie.

Na przykład:

• Ile pracodawca płaci za godzinę brutto, jeśli za sto dziesięć godzin zapłacił do ręki 1290 zł, a stawka podatku wynosi 19 % ?
• 
  Ile farby potrzeba na kwadratowy pokój o powierzchni 8 metrów i wysokości 2.40, jeśli na metr ściany trzeba 7 l ?
• 
  Ile pali samochód na 100 km, jeśli jechał dwie godziny z prędkością 140,
  a zapłaciliśmy 26 zł za benzynę po 6.10 zł za litr ?

Czy czegoś to Wam nie przypomina ? No tak - zadania tekstowe ! Przychodzą na myśl słynne pociągi ze stacji A do stacji B, ale w dzisiejszych czasach założenie o stałej prędkości pociagu jest rażąco nierealistyczne ...

Znane są też następujące anegdotyczne zagadki:

• Cegła waży kilo i pół cegły, ile ważą dwie cegły ?
• Kapelusz z piórkiem kosztuje dwa dwadzieścia. Kapelusz jest droższy od piórka o dwa złote; ile kosztuje piórko ?
  

Rozwiązywanie takich zadań tekstowych składa się z dwóch etapów: z ułożenia równania i z jego rozwiązania. Omówię to na przykładzie owej cegły i piórka, ponieważ zadanie to łatwo zobrazować wizualnie. Po pierwsze : szukamy równania. Zadanie o cegle ukrywa przed niewprawnym czytelnikiem poszukiwane równanie, bo jest wypowiedziane zwięźle, nie zawiera sformułowań "równa się, jest równe", a pytanie jest włączone w treść. Aby je rozplątać, należy się skupić, wysilić, uspokoić (to najważniejsze) i wyobrazić sobie całą rzecz plastycznie:

Może - zamiast wypisywania równania, które tu zobrazowano, przejdziemy od razu do jego rozwiązania - na rysunku, bez zapisu algebraicznego. Mamy "sytuację szalkową", tzn. jakąś wagę, na której coś leży, a waga jest w równowadze. Będziemy się starali wyobrazić takie operacje, które doprowadzą nas do końca GRY . Bo to jest GRA - zdejmuj lub wkładaj coś na wagę w taki sposób, aby dojść do sytuacji, gdy na jednej szalce są dwie cegły (nie więcej i nie mniej), na drugiej pewna liczba odważników (ale żadnych cegieł), a waga jest w równowadze. Szukamy zatem przejścia z sytuacji początkowej do następującej sytuacji końcowej:

Nie wiemy ile odważników będzie po prawej stronie (to jest nasze pytanie - ile ważą dwie cegły, stąd wielokropek na prawej szali !), nie wiemy też ile będzie potrzeba kroków. Dozwolone operacje nie powinny wychylić wagi ze stanu równowagi.

NIE WOLNO więc:

• (zasada 1) zdejmować ani kłaść niczego tylko po jednej stronie wagi

WOLNO zaś:

• (zasada 2) po obu stronach wagi położyć lub zdjąć równoważne ciężary
• (zasada 3) zamienić szale miejscami

Oto jak mogłyby wyglądać możliwe próby:

Na obie szalki dołożyliśmy po cegłówce, ale chyba nie wiemy, co dalej ... Może spróbujemy inaczej, dołożymy po półtorej cegłówki:

... i co dalej ? Nie bardzo wiemy ... W takim razie spróbujmy odejmować:

Ściągamy z obu szalek po połówce cegłówki:

A w tym miejscu zauważmy, że skoro obie strony są równoważne, możemy obie podwoić i wtedy równowaga zostanie zachowana !

I znowu !

I mamy nasze rozwiązanie.

Nasze wagi szalkowe, to równania. Odważniki to liczby, a cegły to niewiadome, na przykład X . Sytuacja wyjściowa odpowiada równaniu:

X = 1 + ½ X

A kroki naszego rozwiązania zapisuje się następująco:

X = 1 + ½ X

½ X = 1

X = 2

2 X = 4

A teraz kapelusz i piórko. To zadanie można rozwiązać przy pomocy układu dwóch równań. Zasada jest taka sama. Należy wyobrazić sobie dwie wagi i operacje na nich (co prawda mowa tu o cenie, nie o wadze, więc pewnie trzeba by wyobrażać sobie jakieś cenniki, albo faktury ...). Mamy dwie niewiadome, ale nic nam to nie szkodzi. Dotąd manewrujemy ciężarami, aż na lewej szalce zostanie to, o co chodzi (w tym wypadku P) a na prawej jakaś liczba bez niewiadomych.

K + P = 2.20     ( Kapelusz z piórkiem kosztuje 2.20 )

K = P + 2     ( Kapelusz jest droższy od piórka o 2 złote )

Wkładamy wszystko na jedną wagę (dodajemy równania stronami):

2 K + P = 4.20 + P

Ściągamy z obu szalek piórko:

2 K = 4.20

Dzielimy to na pół:

K = 2.10

Z tekstu zadania wnioskujemy, że: P = 0.10

JavaScript jako język funkcyjny

JavaScript, język znany powszechnie jako wbudowana maszyna skryptowa przeglądarek webowych, jest kompletnie niedoceniany jako język programowania. Tymczasem jest to zgrabny i mały, ale bardzo elastyczny język dynamiczny. Obsługuje funkcje jako obiekty pierwszej klasy, domknięcia (closures) i funkcje anonimowe. To sprawia, że jest pełnoprawnym członkiem rodziny języków funkcyjnych, a ponieważ jego składnia jest prosta i zbliżona do C, posiada wielką siłę wyrazu, niektórzy zgodzą się nawet, że większą niż języki obiektowe oparte na klasach.

Sam język ani standardowa biblioteka nie posiada wielu udogodnień, ale moc wyrazu JavaScript (może należałoby pisać ECMAScript, ale w dalszym ciągu pozwolę sobie konsekwentnie używać tej pierwszej nazwy) jest tak duża, że potrzebne mechanizmy łatwo definiujemy.

Jako pierwszy przykład rozpatrzę iteratory. Chcemy stworzyć obiekt pozwalający na łatwe indeksowanie tablic, a w przyszłości będący wzorem dla ogólniejszych mechanizmów (wykorzystam go poniżek opisując implementację teoriomnogościowych zbiorów). Nasz iterator to funkcja, która po utworzeniu ustawia się na początku sekwencji, każde jej wywołanie generuje kolejny element, a gdy sekwencja się skończy, zwraca obiekt niezdefiniowany:

function iterator( arr ) {
        var index = 0;

        return function() {
                if ( index >= arr.length )
                        return undefined;
                return arr[ index++ ];
        }
}

Funkcja "iterator" jest konstruktorem iteratora, zamyka tablicę "arr" i zmienną "index" w domknięciu i tworzy funkcję używającą tych obiektów. Rezultatem wywołania funkcji "iterator" jest właśnie iterator. Jego pierwsze wywołanie zwraca pierwszy element tablicy, kolejne wywołania zwracają kolejne elementy. Na przykład:

var it = iterator( [1,2,3,4] );
for ( x=it(); x != undefined; x=it() )
{
     print( x );
}

Taki kod wypisze zawartość tablicy.

Tak skonstruowany iterator jest obiektem-funkcją. Widzimy, że definicja nasza była zwięzła i przejrzysta, dzięki domknięciom i funkcjom pierwszej klasy.

Biblioteki języków obiektowych zawierają definicje różnorakich kolekcji, list, kolejek, wektorów, map itp. Postanowiłem skonstruować na próbę zestaw funkcji i obiektów JavaScript odzwierciedlających podstawowy rachunek aksjomatycznej teorii mnogości. Użytkownicy Javy czy STL z pewnością nie będą pytać o celowość definiowania tak ogólnych mechanizmów.

Nasze zbiory mogą zawierać dowolne elementy (w końcu po to JavaScript jest językiem o słabej typizacji, żeby z tego faktu korzystać). Dla każdego z nich musi istnieć sposób (funkcja? metoda?) na określenie przynależności dowolnego obiektu. Poza tym chcemy mieć możliwość wykonywania takich podstawowych operacji jak dodawanie, selekcja podzbioru (wybór elementów spełniających podany predykat), tworzenie zbioru potęgowego. Siła programowania funkcyjnego polega na tym, że używając kilku prostych pojęć budujemy bardziej złożone, robiąc to prawie tak, jak definiuje się je w matematyce.

Załóżmy na początek, że zbiór jest reprezentowany przez funkcję przynależności. Wywołana z dowolnym argumentem powinna zwrócić wartość logiczną zdania "argument należy do tego zbioru". Używając tej konwencji definiujemy łatwo:

1) zbiór pusty:

   function  empty() {
    return false
   }

2) sumę zbiorów:

  function  sum( a, b ) {
    return  function( x ) {
     return a( x ) || b( x );
    }
   }

Tutaj już użyliśmy domknięcia, na razie sprawa jest prosta i piękna.

3) podzbiór elementów spełniających predykat P:

function  subset( a, P ) {
    return  function( x ) {
     return  a( x ) && P( x );
    }
   }

Tu widzimy, że reprezentacja zbioru jest tożsama z predykatem, a operacja "subset" z częścią wspólną.

Problem pojawia się w momencie, gdy próbujemy utworzyć zbiór potęgowy. Zbiór potęgowy danego zbioru X jest to zbiór wszystkich podzbiorów zbioru X. Zbiór jest podzbiorem innego, gdy zawiera się w nim. Zatem funkcja przynależności to zawieranie, a zatem:

4) zbiór potęgowy:

function  power( a ) {
    return function ( x ) {
     return includes( a, x );
    }
   }

Co jednak oznacza stwierdzenie, że zbiór a zawiera zbiór x ? Oznacza to, że ich część wspólna jest równa x !

5) zawieranie:

   function  includes( a, x ) {
    return  equals( subset( a, x ), x );
   }

A co oznacza równość zbiorów ? Aby zdefiniować ten predykat musimy albo posłużyć się zawieraniem, co spowoduje nieskończoną rekursję, albo wyliczyć wszystkie elementy. Rozszerzamy więc reprezentację zbiorów o funkcję zwracającą iterator. Pozwoli to wyliczyć wszystkie elementy i sprawdzić ich przynależność. Nasz zbiór jest więc dwójką składającą się z funkcji "contains" - będącej odpowiednikiem funkcji przynależności - i funkcji "iterator" zwracającej iterator ustawiony na pierwszy element zbioru, gwarantujący jednokrotne wyliczenie każdego elementu.

Teraz zbiór pusty wygląda tak:

1a) Zbiór pusty:

var empty = {
 contains:function() {return false},
 iterator:function() {return function(){return undefined}}
}

2a) Suma jest nieco bardziej skomplikowana:

function sum(a, b) {
 return {
  contains:function( x ) {return a.contains(x) || b.contains(x)},
  iterator:function()    {
   var i1 = a.iterator();
   var i2 = b.iterator();
   return function() {
    var x = i1();
    if ( x == undefined ) {
     while (true) {
      var next = i2();
      if ( next == undefined ) return undefined;
      if ( a.contains(next) ) continue;
      return next;
     }
    }
    else {
     return x;
    }
   }
  }
 }
}

Komplikacja bierze się z konieczności zagwarantowania braku powtórzeń w iteratorze. Iterator sumy domyka dwa iteratory składników, wyczerpuje pierwszy, a potem używa drugiego sprawdzając, czy zwrócony element nie był już wyliczony wcześniej.

3a) podzbiór elementów spełniających predykat P:

function subset( a, p )
{
 return {
  contains:function ( x ) {
     return a.contains( x ) && p( x );
    },
  iterator:function () {
     var it = a.iterator();
     return function() {
      var x;
      while ( true ) {
       x = it();
       if ( x == undefined ) return undefined;
       if ( p( x ) ) return x;
      }
     }
    }
 };
}

I wreszcie sprawca zamieszania, zbiór potęgowy:

4a) Zbiór potęgowy:

function power( a ) {
 return {
  contains:function( x ) {
     return includes( x, a );
    },
  iterator:function() {
     var div = divide( a );
     if ( div.head == undefined )
      return singleton( empty ).iterator();
     var tail_pow = power( div.tail );
     var tail_pow_iterator1 = tail_pow.iterator();
     var tail_pow_iterator2 = tail_pow.iterator();
     return function() {
      var x;
      x = tail_pow_iterator1();
      if ( x != undefined )
       return x;
      x = tail_pow_iterator2();
      if ( x == undefined )
       return undefined;
      return sum( singleton( div.head ), x );
     }
         }
 }
}

Pełne źródła tych procedur można pobrać tu: sets.txt, tam też znajdują się pomocnicze procedury "includes" i "divide". Ta druga posłużyła do wydzielenia jednego elementu i reszty - z dowolnego zbioru. Dzięki temu zbiór potęgowy mógł zostać zdefiniowany rekursywnie.

A teraz proszę popatrzeć, jak to ładnie działa:

Oto wynik działania programu testowego:

Zbior 4 - elementowy:
{1, 2, 3, 4}
Jego zbiór potęgowy:
{{}, {4}, {3}, {3, 4}, {2}, {2, 4}, {2, 3}, {2, 3, 4}, {1}, {1, 4}, {1, 3}, {1, 3, 4}, {1, 2}, {1, 2, 4}, {1, 2, 3}, {1, 2, 3, 4}}
Zbiór podzbiorów właściwych:
{{4}, {3}, {3, 4}, {2}, {2, 4}, {2, 3}, {2, 3, 4}, {1}, {1, 4}, {1, 3}, {1, 3, 4}, {1, 2}, {1, 2, 4}, {1, 2, 3}}
Albo:
{{4}, {3}, {3, 4}, {2}, {2, 4}, {2, 3}, {2, 3, 4}, {1}, {1, 4}, {1, 3}, {1, 3, 4}, {1, 2}, {1, 2, 4}, {1, 2, 3}}
Czy zbiór jest jednoelementowy ?
{} :  false
{1} :  true
{1, {}} :  false
Istnienie elementu o podanej wlasnosci:
{1, 2, 3, 4} , 3:  true
{1, 2, 3, 4} , 100:  false
Kwantyfikator ogólny:
Czy zbior jest dwuelementowy ?
{} :  false
{1} :  false
{{}, {1}} :  true
{1, 2, 3, 4} :  false

Warto zwrócić uwagę na sposób definiowania kwantyfikatorów - funkcje anonimowe (w notacji lambdapodobnej) dają możliwość nazywania zmiennych związanych pod kwantyfikatorem, więc da się tego używać bez wielkiego wysiłku. Porównawszy to z kodem, który trzebaby napisać w C++ używając <functional> widzimy moc wyrazu JavaScript.

I kto dalej twierdzi, że JavaScript to język do robienia animowanych buttonów w internecie ? No kto ?

szablony w C++

Mechanizm szablonów w C++ umożliwia deklarowanie klas i funkcji sparametryzowanych typami lub wartościami. Klasa w C++ wprowadza przestrzeń nazw, w której można deklarować obiekty statyczne - daje to możliwość używania szablonów do deklarowania innych obiektów języka, nie tylko klas i funkcji - bezpośrednio nie byłoby to możliwe. Nie można na przykład zdefiniować szablonu tablicy, o tak:

template <class T>
T table[100];

Ale można uzyskać pożądany efekt w taki prosty sposób:

template <class T>
class t {
        public:
        static T table[100];
};

template <class T>
T t<T>::table[ 100 ];

Podobnie można postąpić z innymi kontrukcjami: Np. wyliczenie:

template <int N>
class t {
        public:
                enum en {
                        START=N,
                        STOP
                };
};

Szablonów można użyć do wielu nieoczywistych sztuczek. Oto jak można sprawdzić, czy dwa wyrażenia są tego samego typu:

template <class T>
bool same_type(const T&, const T&) {
        return true;
}

template <class T1, class T2>
bool same_type(const T1&, const T2&) {
        return false;
}

int main()
{
        std::cout << same_type(1, 2) << '\n';
        std::cout << same_type(1, 2.1) << '\n';
}

Kompilator oczywiście całkowicie optymalizuje taką funkcję - zamienia ją na stałą.